结果的框架

风险前景的特点表现在它们可能的结果以及产生这些结果的概率方面。然而，同样的选择会以不同的方式来构架或描述。例如，一次赌的可能结果可以被构架成现状的获得或损失，或是包含最初财富的资产状态。不变性要求不能因为对结果描述的不同而改变自己的偏向。下面的这两个问题违反了这个要求。N表示每个问题的受试者总数，括号里是选择每个选项的人数比例。

问题1（N=152）：设想美国可能爆发一种异常的亚洲疾病，这种疾病可能导致600人死亡。有两种方案来应对疫情，假设下面是对每种方案结果准确的科学预测：

如果采取方案A，可救治200人。（72%）

如果采取方案B，有1/3的概率救治600人，2/3的概率无人获救。（28%）

你会选择哪种方案？

问题1的表达模式可作为此事件的一个参考状态，即该疾病会夺去600条生命。两种方案的结果包括这种参考状态以及通过被救者的数量而量化得来的收益情况。就像期待的那样，偏好是一种风险规避：绝大多数受试者更愿意选择能保证有200人获救的方案，而不是有1/3的可能性救600人的方案。现在来考虑另一个问题，还是同样的情况，但两种方案用的是另一种方式表述：

问题2（N=155）：

如果采取方案C，400人死亡。（22%）

如果采取方案D，1/3的概率没有人死，有2/3的概率600人全部死亡。（78%）

很容易看出问题2中的方案C和D与问题1中的方案A和B在本质上没有差别。然而问题2中假设的参考点是没有人会因为该疾病而死亡。最好的结果是维持该参考状态，其相对的情况是因该疾病致死的人数来量化的损失。用这些参考状态来评估作出的选择可表明，人们会偏向于赌一把（方案D）的风险追求，而不是肯定会丧失400条性命的风险追求。实质上，在第二个问题中的风险追求比在第一个问题中的风险规避代价更大。

没能遵守不变性这一现象非常普遍，且难以克服。这在经验丰富的受试者和初级受试者中都很常见，即使相同的受试者在几分钟内回答这两种问题，也无法消除这一现象。面对两种相互矛盾的回答，受试者也时常不解。但即使再读一遍该问题的陈述，他们也会在“生命拯救”的说法中选择风险规避，在“生命死亡”的说法中选择风险追求。而且他们在两种说法中都希望能遵守不变性，且给出一致的回答。在他们不断地迎合下，框架效应更像是感觉错觉而不是计算上的错误。

下列问题引出了违反理性决策的主要要求的偏向。

问题3（N=86）：请在下列选项中作出选择：

E：25%的概率赢得240美元，75%的概率失去760美元。（0）

F：25%的概率赢得250美元，75%的概率失去750美元。（100%）

👓 落·霞+读·书=- l u o x i a d u s h u . c o m -=-

很容易看出F比E更占优势。实际上，所有的受试者也都是这样选择的。

问题4（N=150）：设想你需要同时对下面两个问题做出决策。

先看一下两个决策，之后选出你偏爱的那一项。

决策（1）在下列两者中选择：

A.肯定会得到240美元。（84%）

B. 25%的概率得到1000美元，75%的概率什么也得不到。（16%）

决策（2）在下列两者中选择：

C.肯定会损失750美元。（13%）

D. 75%的概率损失1 000美元，25%的概率什么也不损失。（87%）

通过前面的分析可以看出，在第一个决策中，大多数受试者会对确定的事选择风险规避；更多的受试者在第二个决策中选择风险追求，而不是确定的事。事实上，73%的受试者选择A和D，而只有3%的受试者选择了B和C。同样的结果模式也出现在问题的另一种说法中，在这种说法中，大学生们选择了他们能够真正参与的博一把。

受试者会同时考虑问题4中的两个问题，因此，相对于B和C，他们会偏向于A和D。然而，受试者的偏向（A和D）往往受放弃的选择的控制。若把肯定会得到的收益（选项A）增加到D选项上，会产生有25%的概率赢得240美元和75%的概率失去760美元的结果。这正是问题3中的选项E。同样，把750美元确保的损失（选项C）增加到B选项上，会产生25%的概率得到250美元和75%的概率失去750美元的结果，这也正是问题3中的F选项。因此构架的敏感性以及S形的价值函数在一些需要同时做出决策的事件中与主导因素相违背。

能运用这些结果的地方并不理想：不变性从规范上来看是至关重要的，直觉是很吸引人的，但从心理学角度看却无法实现。我们只设想了保证不变性的两种方式。第一种就是采取可将任何问题、实质等同的表达方式转化成完全一样的常规表述。我在给经济系的学生上课时，常会将这点作为最基本的原理告诫他们，他们应该在思考每一个决策问题时，从总值的角度考虑，而非仅从收益和损失上考虑。这样的表述可避免违背在先前问题中提到的不变性，但执行起来却很难。除了特殊情况，也就是从获得和损失的角度考虑钱财结果比从当前的财富状态考虑更普遍。此外，风险前景的常规表述需要计算同时出现的决策（例如问题4）的所有结果，而计算这些同时出现的决策的难度超过了对简单问题直觉上的计算。在其他条件下用常规表述更困难，这些条件包括安全性、健康性或生活质量。我们是否应该建议人们，通过计算因某种疾病致死的总数，或因研究中某种特殊疾病而致死的人数，去评估公共卫生政策（例如问题1和2）？

另一种可以保证不变性的方法是通过保险精算的结果来评估某项选择，而非通过心理学的结果来评估。在人们的生活中，保险精算的准则有一定的吸引力，但对于涉及钱的决策而言，这样的准则明显不够。应该说，该准则在伯努利时期就被意识到了，而且对于缺少客观量度标准的结果完全不适用。总之，构架不变性很难被预测，而且人们在某个特殊选择中的自信不能确保其在另外一个框架下还会做出同样的决策。因此，用多种方法来构架决策问题的行为来测试偏向的稳定性是个不错的方法。

概率的心理物理学

到目前为止，我们假设伯努利的期望原则所依据的是某种不确定前景的价值或效用，该原则是通过增加每种可能结果的效用而得来的，每个结果的效用又都是通过概率来加以权衡的。为了测试这个假设，我们再从心理物理学角度出发。将当前的状态价值设为零，想象有份价值300美元的收益，我们将这份收益的价值设为1。现在假设你只有一张彩票，且该彩票的单次奖励是300美元。这张彩票的价值会怎样随着赢得奖励的可能性函数而改变？除了赌一把的效用外，这种前景的价值一定会在零（当赢得的概率为零时）和1（确定赢得300美元）之间变化。

按照直觉，彩票的价值并不是获胜概率的线性函数，正如期望原则推导出的那样。从零到5%的增长比从30%到35%的增长有更大的影响力，而相对于从95%到100%的增长，影响就显得小了。综合考虑各方面可得出种类—边界效应：即从不可能到可能，或从可能到确定的变化比变化范围内的变化有更大的影响力。这种假设体现在图B–2的曲线上，该曲线以函数的形式标出了对某事件众多可能性的权重。该图最大的特点是关于规定的可能性，决策权重会成回归状态。除了终点附近，获胜的概率每增加0.05，赢得奖励的价值就会增长不到5%。我们接下来要研究的就是在有风险的选择中，对偏向的心理物理学假设的含义。

在该图中，决策权重在很大的范围内要低于相应的概率。过低权衡确定事件的中等或高概率会降低能得到奖励的赌局的吸引力，从而在会有所得的选择中使人们选择风险规避；同样，在损失的情况下，也会通过减弱对赌局中的损失厌恶而选择风险追求。然而，小概率事件常被过高权衡，且非常小的概率不会被过高权衡或完全忽视，使得这个区域内的决策权重很不稳定。对低概率过高权衡推翻了前面描述的规律模式：它提高了风险大的赌注的价值，提高了对于小概率的严重损失的厌恶值。最终，人们通常在未必有收益的情况下选择风险追求，在未必有损失的情况下选择风险规避。因此，决策权重的特点解释了彩票和保险政策吸引人的原因。

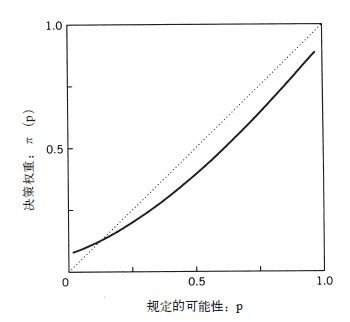
图B-2

决策权重的非线性必然会违背不变性，下列两个问题就说明了这一点：

问题5（N=85）：假想有如下两个阶段的游戏。在第一个阶段，有75%的概率在游戏最后什么也得不到，有25%的概率会进入到第二个阶段。如果你进入第二个阶段，可以在下面两个选项中作出选择：

A.肯定会获得30美元。（74%）

B.80%的概率获得45美元。（26%）

你必须在游戏开始前作出选择，也就是说，要在第一个阶段结果出来前选择。

问题6（N=81）：请在下面两个选项中作选择：

C.25%的概率获得30美元。（42%）

D.20%的概率获得45美元。（58%）

由于在问题5中有25%的概率进入到第二个阶段，选项A有25%的概率获得30美元，选项B有80%（0.25×0.80 = 0.20）的概率获得45美元。因此，问题5和问题6在概率和结果方面是相同的。不过，这两种说法的偏向却不同：在问题5中，绝大多数人更喜欢获得小数目钱的高概率选择；而在问题6中，情况却正相反。现实和假设的收益（当前，其结果用钱来表示），生命的拯救和丧失，以及概率过程的非连续表示都已经证实了这种与不变性的违背。

我们认为，不变性之所以被证实不成立是由于两种因素的相互作用：即概率的构架和决策权重的非线性。具体说，我们认为，人们会忽略问题5中的第一个阶段（不管是否已经做出决策，都会产生相同的结果），且只专注于进入第二个阶段后会发生什么。当然，在这种情况下，如果人们选择A，肯定会有所获得；但如果人们更愿意赌一把，就会有80%的概率获得收益。的确，在需要作出连续选择的问题中，人们的选择会和在肯定会获得30美元且有85%的概率获得45美元间的选择相同。因为相比有一般或较高概率的事件来说，确定事件会被过高权衡，肯定会获得30美元的选项就比需要连续做出决策的问题选项更具吸引力。我们将这种现象称为虚假确定性效应，因为实际上不确定的事件在被权衡时会被看成是确定的。