第十二章 好人终有好报 · 2
这里,我们不关心某一个策略是否优于另一个策略。我们只关心哪个策略在与15个对手博弈后,最终赢得最多的“钱”。在这里,“钱”指的是赢得的分数。相互合作的奖赏为3分,背叛的诱惑为5分,互相背叛的惩罚为1分(相当于我们早先例子中的轻判),失败的代价为0分(等同于之前例子中的重罚)。
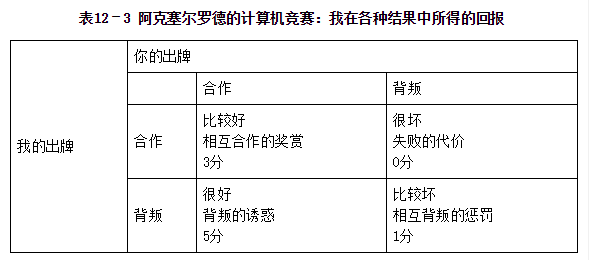
无论是哪一种策略,理论上它们能得到的最高分都是15 000分(每一回合5分,15个对手共有200回合),最低分则是0分。不用说,这两个极端都没有实现。实际上,一个策略如果能超过15个对手中的平均水平,最多也只能获得比600分高出一些的分数。因为如果对手双方决定他们持续合作,每人在200场博弈中都能得到3分,总共便是600分。我们可以将600分作为基准分,将所有分数表达为600分的百分比。这么算来,理论上的最高分将是166%(1 000分)。但事实上,没有任何一个策略的平均分超过600分。
要知道,竞赛中的博弈者并不是人类,而是计算机事先设定好的程序。而基因则在这些程序的作者里事先设定了“程序”,使得它们身体力行地扮演同样的角色(想想第四章中的计算机对弈与“仙女座”超级计算机)。你可以将这些策略想象成这些作者的微型代理。虽然一个作者原本可以提交一个以上的策略,但这其实是作弊,这表示作者将在竞争本身中加入策略,使得其中一个角色从另一个角色的牺牲中得到合作的好处。阿克塞尔罗德应该不会接受这一点。
💄 落^霞^读^书lu o xi a d u sh u . com *
交上来的有一些很聪明的策略,当然它们远没有其作者聪明。然而,最后胜出的策略却是一个最简单的、而且看起来最不聪明的一个。这个策略称为“针锋相对”(Tit for Tat),它来自多伦多一位著名心理学家和博弈学家阿纳托尔(Anatol Papoport)教授。这个策略在第一回合时采取合作行动,然后在接下来的所有步骤里,只是简单复制对手上一步的行动。有了“针锋相对”策略的博弈将如何进行呢?一如寻常,下一步的出牌完全取决于对手。假设另一对手也选择了“针锋相对”的策略(每一个策略不止与其他14个对手竞争,也与自己本身博弈),双方都选择以“合作”而开场。第二步中,双方都复制对方上一步的策略,仍然采取“合作”。这样,博弈双方持续合作,直到游戏结束,双方都能获得100%的600分基准分。
那么,假设“针锋相对”与另一个策略“老实人探测器”(Native Prober)开始博弈。事实上,“老实人探测器”并没有出现在阿克塞尔罗德的博弈竞赛中,但它依然是一个富有指导性的策略。这个策略基本等同于“针锋相对”,但每隔一会儿,比如在每十步中任意选择一步,这个策略会打出恶意的“背叛”牌,而获得最高的分数“背叛的诱惑”。如果“老实人探测器”不打出其试探的“背叛”牌,博弈双方便是两个“针锋相对”,打出一场漫长且互利的合作牌,彼此安稳地获得100%的基准分。但突然间(假设在第8回合),“老实人探测器”出其不意地“背叛”了。“针锋相对”却依然不知情地坚持“合作”,也便只能付出“失败者的代价”,得到0分。而“老实人探测器”则能得到最高成绩5分。但在下一步里,“针锋相对”开始报复,复制了对手上一步的行动,打出了“背叛”牌。而“老实人探测器”则盲目地继续原本设定的程序,复制对手上一步的“合作”牌。于是它只能获得0分,而“针锋相对”则得到5分。再下一步,“老实人探测器”极其不公正地又开始了报复,“背叛”了“针锋相对”。反之亦然。在每一轮交替报复的回合里,双方各自平均获得2.5分(5分与0分的平均值)。这依然低于双方持续双向合作所能轻而易举获得的3分(这也是本章前文中尚未解释的“特殊情况”的原因)。于是,当“老实人探测器”与“针锋相对”开始博弈,双方都未能获得两个“针锋相对”博弈时所得的分数。而如果“老实人探测器”互相对弈,其结果只可能更坏,因为这种以牙还牙的冤冤相报可能开始得更早。
让我们再来考虑另一个叫“愧疚探测器”(Renwrseful Prober)的策略。这个策略有点类似于“老实人探测器”,但它还加以主动终止循环于双方间的交互背叛。这便需要一种比“针锋相对”或“老实人探测器”更长的记忆。“愧疚探测器”能记住自己是否刚刚主动“背叛”,或者只是为了报复。如果是后者,它便“愧疚地”让对手得到一次反击的机会,而不加以报复。这便将此循环报复行为终结在萌芽状态。如果你在想象中旁观“愧疚探测器”与“针锋相对”的博弈,你会发现可能的循环报复行动不攻自破。博弈中大部分时间都采取互相合作,使得双方都能获得相应的高分。在与“针锋相对”的博弈中,“愧疚探测器”能获得比“老实人探测器”更高的分数,但依然没有“针锋相对”与自己对弈的分数高。
阿克塞尔罗德的竞赛里还有一些比“老实人探测器”与“愧疚探测器”更为复杂的策略,但它们平均分都比“针锋相对”低。事实上最失败的策略(除了随机)是最复杂的那一个,作者为“匿名”。这个作者引发了一些饶有兴趣的猜测:五角大楼的高层?中央情报局的首脑?国务卿基辛格?阿克塞尔罗德自己?我们也许永远也不会知道。
不是每个策略的细节都值得研究,这本书也不谈计算机程序员的创造力。但我们可以给这些策略归类,并检验这些类别的成功率。阿克塞尔罗德认为,最重要的类别是“善良”。“善良”类别指的是那些从不率先背叛的策略。“针锋相对”便是其中一个例子。它虽然也采取“背叛”的行动,但它只在报复中这么做。“老实人探测器”与“愧疚探测器”也偶尔采取“背叛”,但这种行为是主动起意挑衅的,属于恶意的策略。这场竞赛中的15个策略中,有8个属于“善良”策略。令人吃惊的是,策略中的前8名也是这8个善意的策略。“针锋相对”的平均分504.5分,是我们600分基准分中的84%,一个很好的分数。其他“善良”策略所得分数要比“针锋相对”少一些,从83.4%到78.6%不等。排名中接下来的分数则是由格雷斯卡普(Graaskamp)所获得的66.8%,与高分们有很大差距,而这已经是所有恶意策略中的最高分了。令人信服的结果表明,好人在这个博弈中可以胜出。
阿克塞尔罗德的另一个术语则是“宽容”。一个宽容的策略只有短期记忆。虽然它也采取报复行为,但它会很快遗忘对手的劣迹。“针锋相对”便是一个宽容的策略,面对背叛时它毫不手软,但之后则“过去的让它过去”。第十章中的“斤斤计较者”则是一个完全相反的例子。它的记忆持续了整个博弈,永不宽恕曾经背叛过它的对手。在阿克塞尔罗德的竞赛中,有一个策略与“斤斤计较者”完全相同,由一位名叫弗里德曼(Friedman)的选手提供。这一个“善良”而绝不宽恕的策略结果并不算佳,成绩在所有“善良”策略里排倒数第二。即便对手已经有悔改之意,它不愿意打破相互背叛的恶性循环,因此无法取得很高的分数。
“针锋相对”并不是最宽容的策略。我们还可以设计一个“两报还一报”(Tit for Two Tats)的策略,允许对手连续两次背叛后才开始报复,这似乎显得过分大度坦荡了。阿克塞尔罗德算出,只要在竞赛中有“两报还一报”策略的存在,它便一定会获得冠军,因为它可以有效避免长期的互相伤害。
于是,我们算出了赢家策略的两个特点:善良与宽容。这几乎是一个乌托邦式的结论:善良与宽容能得到好报。许多专家曾试图在恶意策略里耍点儿花招,认为这可能得到高分。即使那些提交“善良”策略的专家,也未曾敢如“针锋相对”一般宽容。所有人都对这个结论十分惊讶。
阿克塞尔罗德又举办了第二次竞赛。这次他收到了62个策略,再加上随机策略,总共便有了63个策略。这一次,博弈中的回合数不再固定为200,而改为开放式的不定数(我之后会解释这么做的理由)。我们依然将得分评判为基准分“永远合作”分数的百分比,不过现在基准分需要更为复杂的计算,并不再是固定的600分。
第二次竞赛的程序员们都得到了第一次竞赛的结果,还收到了阿克塞尔罗德对“针锋相对”与善良与宽容策略获胜的分析。这么做是为了让参赛者们能从某种方向上了解比赛的背景信息,来权衡自己的判断。事实上,这些参赛者分成两种思路。第一种参赛者认为,已经有足够证据证明善良与宽容确实是获胜因素,他们便随即提交了善良与宽容的策略。一位参赛者约翰·梅纳德·史密斯(John Maynard Smith)提交了一个最为宽容的“三报还一报”(Tit for Three Tats)的策略。另一组参赛者则认为,既然对手们已经读过了阿克塞尔罗德的分析,估计都会提交善良宽容的策略。他们于是便提交了恶意的策略,以期在善意对手中占到便宜。
然而,恶意再一次没有得到好报。阿纳托尔提交的“针锋相对”策略再一次成为赢家,获得了满分的96%。而善意策略又再一次赢了恶意策略。前15名中只有一个策略是恶意策略,而倒数15名中只有一个是善意策略。然而,最为宽容的、可以在第一次竞赛中胜出的“两报还一报”策略,这次却没有成功。这是因为本次竞赛中有了一些更为狡猾的恶意策略,它们善于伪装自己,无情地抛弃那些善良的人们。这揭晓了这些竞赛中非常重要的一点:成功的策略取决于你的对手的策略。这是唯一能解释两次竞赛中的不同结果的理由。然而,就像我之前说过的那样。这本书并不是关于计算机程序员的创造力的,那么,是否有一个广泛客观的标准来让我们判断,哪些是真正好的策略?前几章的读者们估计已经开始准备从生物进化稳定策略理论中寻找答案了。
当时的我也是阿克塞尔罗德传播早期结果的小圈子中的一员,我也被邀请在第二次竞赛中提交策略。我并没有参赛,但我给阿克塞尔罗德提了一个建议。阿克塞尔罗德已经开始考虑“进化稳定策略”(EES)这个理论了。但我觉得这个想法太重要了,于是写信给他建议,让他与汉密尔顿(W.D.Hamilton)联系一下。虽然当时阿克塞尔罗德并不认识汉密尔顿,但汉密尔顿正与阿克塞尔罗德在同一所大学——密歇根大学的另一个系里。阿克塞尔罗德迅速联系了汉密尔顿。最终,他们合作的结果是一篇卓越的论文,发表在1981年的《科学》杂志上,也获得了美国科学促进会(AAAS)的纽科姆·克里夫兰奖(Newcomb Cleveland Prize)。阿克塞尔罗德和汉密尔顿除了讨论重复“囚徒困境”在生物学上有趣的例子外,我还觉得他们给予了进化稳定策略方法应有的认可。
让我们来比较一下进化稳定策略与阿克塞尔罗德两次竞赛中的“循环赛”机制。循环赛好比足球联盟中的比赛。每一个策略都与其他策略对战同等次数。策略的最后得分则是它与所有其他策略对弈后的所得总分。如果一个策略想要在竞争中成功,它必须在所有提交的策略中都富有竞争力。阿克塞尔罗德给胜出其他对手的策略定义为“强劲”。“针锋相对”便是一个强劲的策略。但参与竞赛的策略对手们则相当主观,只取决于参赛者所提交的策略水平。这一点使我们相当头疼。阿克塞尔罗德的第一个竞赛里,刚好参赛的策略基本都是善意策略,所以“针锋相对”赢得了竞赛,而如果“两报还一报”参赛了,则会赢了“针锋相对”。但如果几乎所有参赛策略都为恶意策略,情况就不同了。这个假设发生的概率还是很大的,毕竟所提交的14个策略中有6个是恶意策略。假如13个策略全为恶意策略,“针锋相对”则不可能成功,因为“环境”太差了。提交策略的不同,决定了策略所赢得的金钱和它们的排名位置。也就是说,竞赛结果将取决于参赛者的心血来潮。那么,我们如何减少竞赛的主观性呢?答案是:进化稳定策略。